In my previous article I investigated and wrote about A beginners guide to PDF lattice shading and in this article I will be focusing on Coons Shading and color interpolation on any given point of Coons patch.
Let us take a closer look on what information the PDF specs provide on coons shading:
BitsPerCoordinate : number of bits used to represent vertex coordinates.
BitsPerComponent: number of bits used to represent color component.
BitsPerFlag : number of bits used to represent edge flag information, (edge flags are used to define how one patch is connected with another).
Decode : array of numbers which specifies how to map the coordinates and color components into proper range values. PDF’s use this values in order to reduce the file size, therefore retrieved ‘bits per coordinate and bits per component values’ have to be interpreted to actual values using the decode array.
Function : type of functions used to retrieve color mappings. ( more explanation on functions and how it works will be discussed in my next article as it is major area to be covered)
Let us take a closer look on Coons patch
Coons patch is a shape which is made of four cubic bezier curves. Each curve length influences the color value of any given pixel inside a coons patch. 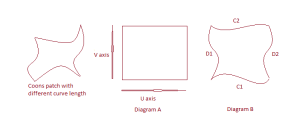
What is the Goal ? What is the formula ?
The goal is to find the color values of any given point(x,y) in the coons patch. Unfortunately there is no formula which retrieves the exact color value of the given coordinate. So it has to be workout with arbitrary value of t in the range of 0 to 1 and apply interpolation formula to find it; so the more t intervals means more accuracy can be obtained.
What is the formula which PDF spec gives
Before performing the calculation the corner points and control points of coons patch needs to be identified, these information can be obtained from stream data and bits per coordinate values.
if we rename 4 cubic curves as C1, C2, D1, D2 then the corner points will be:
C1(0) = D1(0)
C1(1) = D2(0)
C2(0) = D1(1)
C2(1) = D2(1)
Once the corner points and control points are identified, each bezier curves need to be split into equal t intervals. In theory we are splitting a coons into several trapezoids shaped coons.
The Two surfaces can be described has linear interpolations between the boundary Curves.
Along the u axis, the surface SC is defined by:
SC(u, v) = (1 – v) × C1(u) + v × C2(u)
How do you work out this function above ?
Each x, y values need to be calculated in along u axis.
In java the contents inside a for loop may look similar to below in order to obtain above algorithm (Please note : i values depend on t intervals)
float scx = (1 – v) * controlPointsC1[i].getX() + v * controlPointsC2[i].getX();
float scy = (1 – v) * controlPointsC1[i].getY() + v * controlPointsC1[i].getY();
Along the v axis, the surface SD is given by:
SD(u, v) = (1 – u) × D1(v) + u × D2(v)
Calculate x,y values along V axis.
A third surface is the bilinear interpolation of the four corners:
SB(u, v) = (1 – v) × [(1 – u) × C1(0) + u × C1(1) ] + v × [(1 – u) × C2(0) + u × C2(1) ]
calculate x,y values B surface ( B is an imaginary bilinear interpolation surface)
The coordinate mapping for the shading is given by the surface S, defined as:
S = SC + SD – SB
Now perform bilinear interpolation on color values (you can use SB formula for this)
SB(u, v) = (1 – v) × [ (1 – u) × Color1[i] + u × Color4[i] ]+ v × [(1 – u) × Color2[i] + u × Color3[i] ]
Colors have to be interpolated in each components : for example if it is a rgb component variable i takes 3 values and if it is a cmyk color it takes 4 values.
As a result of the above algorithm you will be able to find coordinate and color values for each trapezoids so it is easy to find the color interpolation on any trapezoids now.
I Hope you find this information useful.
Our software libraries allow you to
| Convert PDF files to HTML |
| Use PDF Forms in a web browser |
| Convert PDF Documents to an image |
| Work with PDF Documents in Java |
| Read and write HEIC and other Image formats in Java |